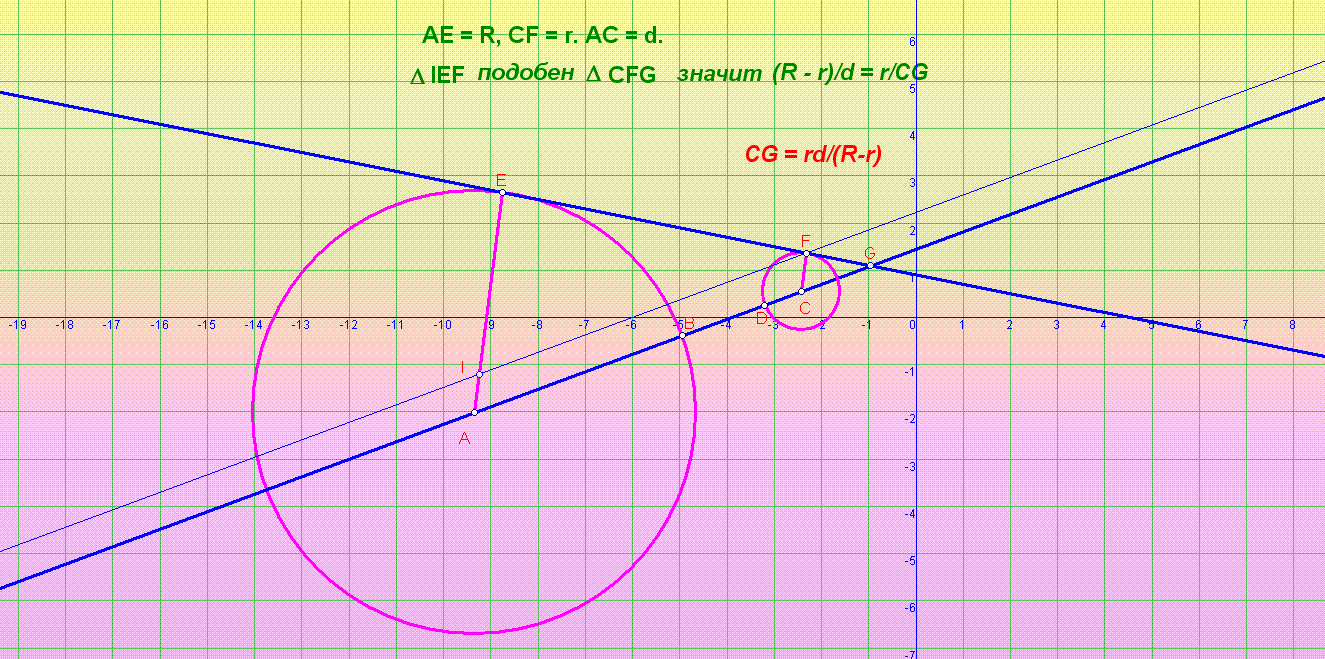
Nasty, я выложил решения двух задач, которые мы не успели решить.
1.На стороне АС остроугольного треугольника АВС найдите такую точку, чтобы расстояние между её проекциями не две
другие стороны было наименьшим.
Решение.
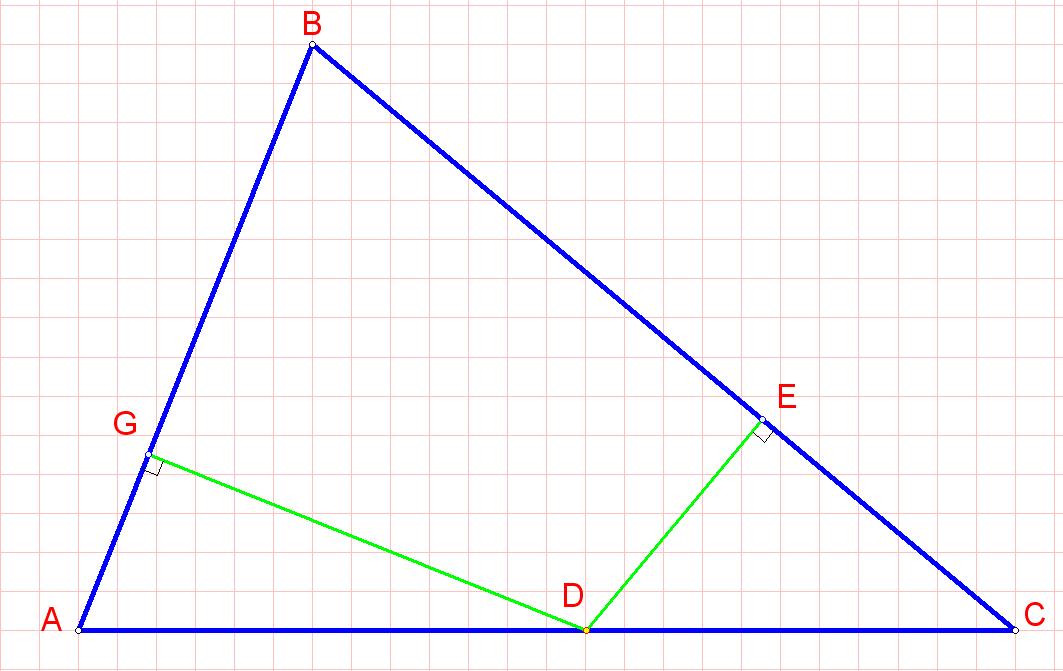
Пусть D - искомая точка. Опустим из точки D перпендикуляры DG и DE на стороны AB и BC. Тогда около четырёхугольника BEDG можно описать окружность, причём диаметр
этой окружности - ВD. Эта окружность является описанной для треугольника GBE. Пусть R - радиус этой окружности. Тогда GE = 2RsinABC = BD sinABC. Т. е. GE - наименьшее,
когда BD наименьшее, т. е. совпадает с высотой треугольника АВС, проведенной из вершины В.
вторую задачку выложу позже. Увы - время...
Вторая задача
2. Две окружности пересекаются в точках А и В. Через точку Р, принадлежащую отрезку АВ, проведена хорда КМ первой окружности и хорда LN второй окружности. Докажите, что точки K, L, M, N лежат на одной окружности.
Решение.
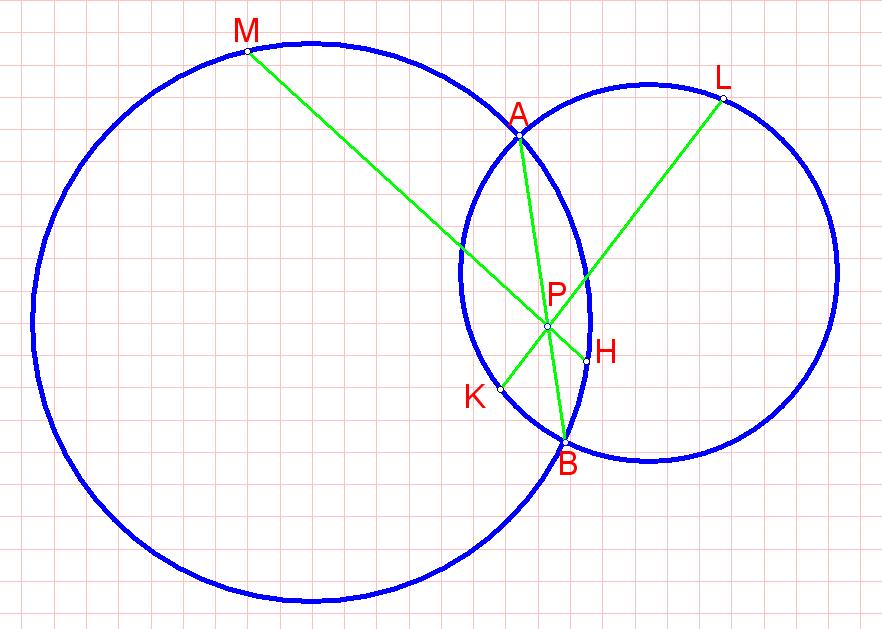
Так как LN и AB - пересекающиеся хорды первой окружности, то AP·PB = LP·PN. Аналогично AP·PB = MP·PK, т. е. LP·PN = MP·PK. Отсюда LP:PK = MP:PN. Следовательно треугольник KLP подобен треугольнику MPN по второму признаку подобия треугольников. Тогда угол KLN равен углу KMN, а это и означает, что точки K, L, M, N лежат на одной окружности.
Да Ben, конечно.
Алина!
В задаче указано, что искать нужно среди простых чисел, то есть среди чисел меньших двадцати, которые делятся нацело только на единицу и самих себя.
То есть: 1, 2, 3, 5, 7, 11, 13, 17, 19.
Таким образом, речь идёт о А92. Но среди них будет 8 в знаменателе, которых будут единицы, т.е. окончательный ответ: А92 - 8 = 8·9 - 8 = 64.
Я знаю, что такого ответа нет и правильный, по мнению авторов 56. Но именно мой ответ правильный. При встрече покажу как всё расписал.
Интегралы.

Второй интеграл

Я нашёл неопределённые интегралы. Пределы подставите сами...
Ряд,